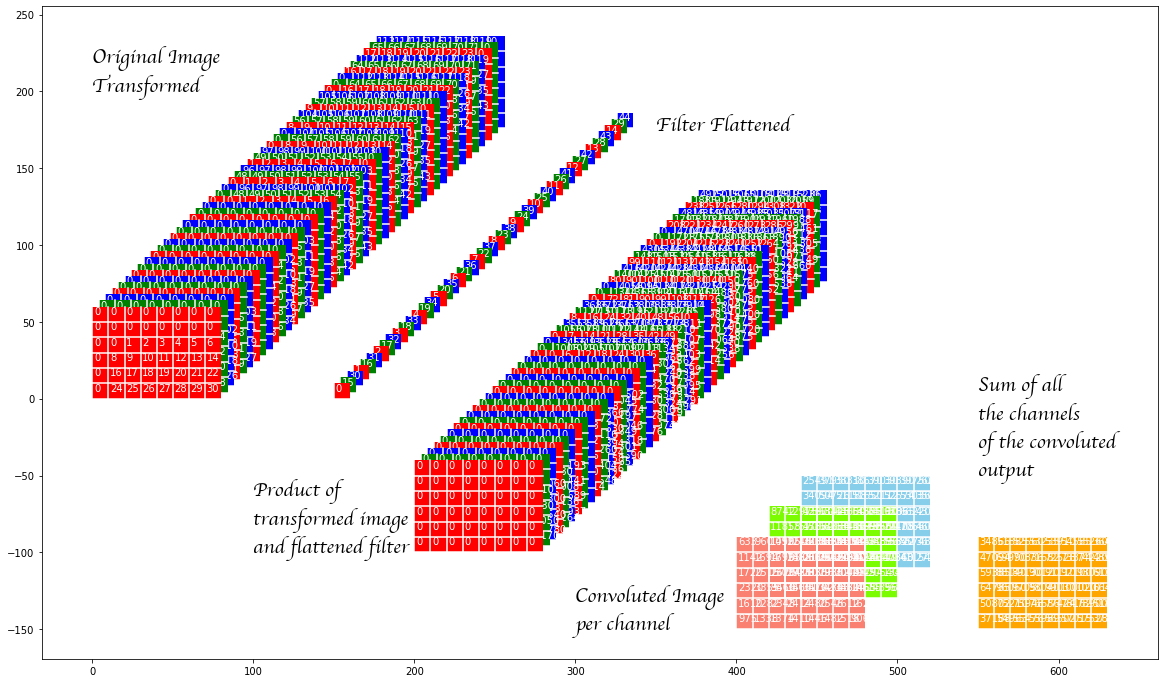
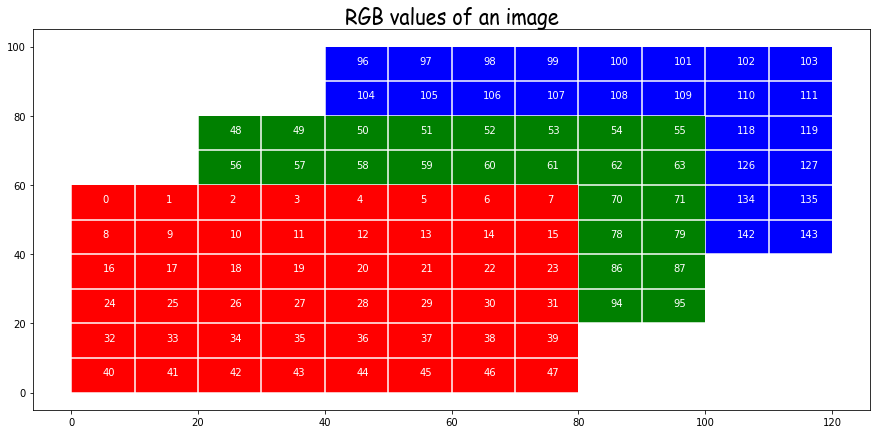
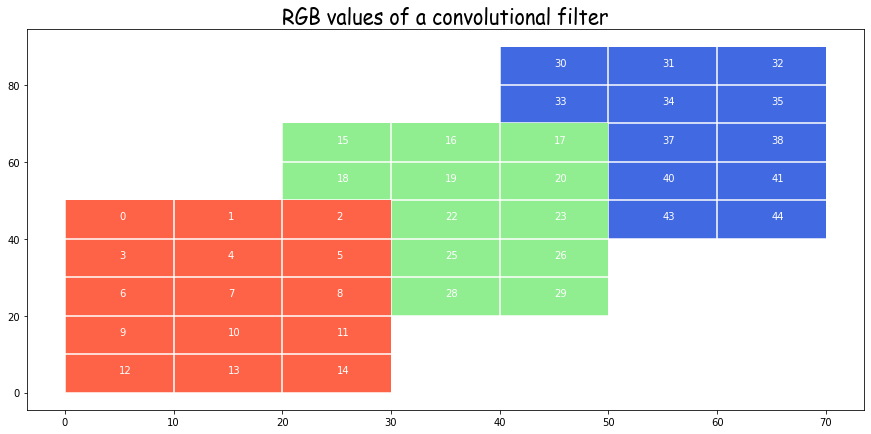
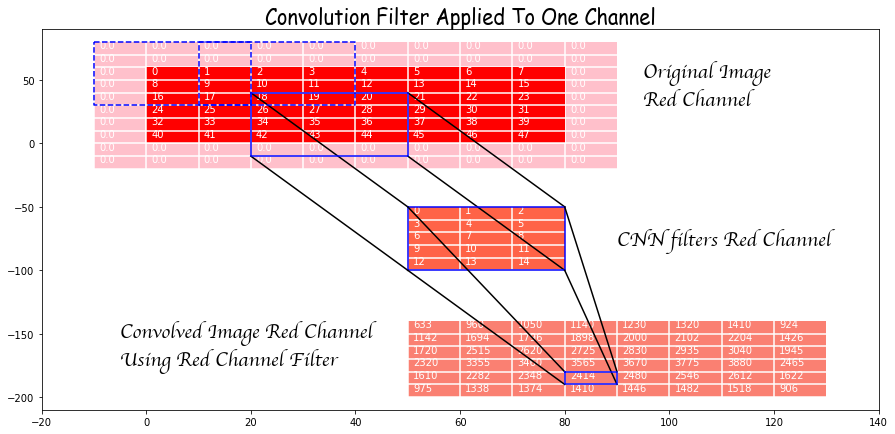
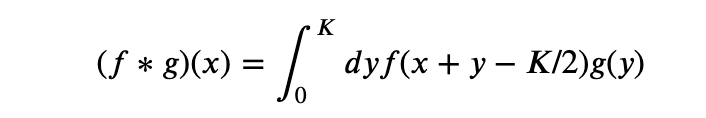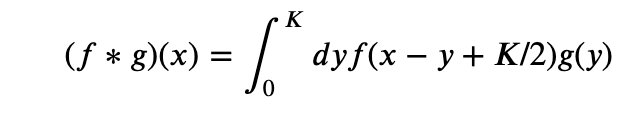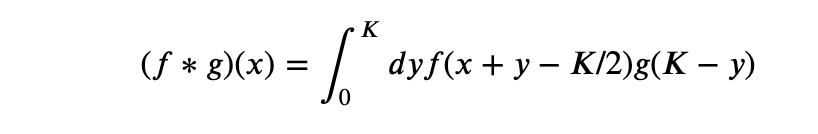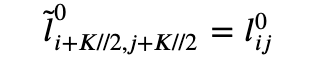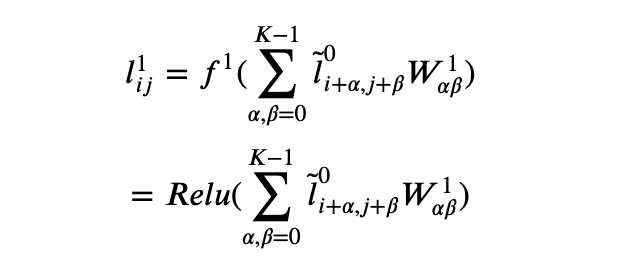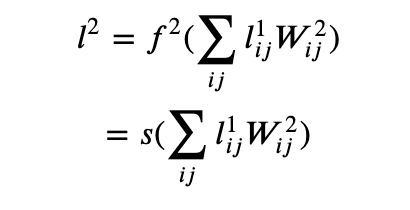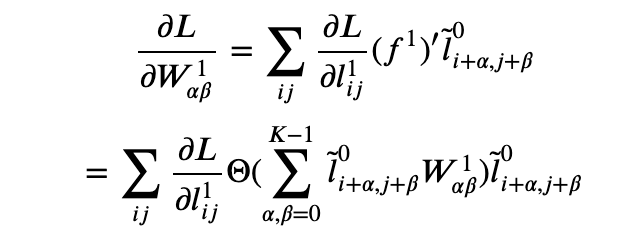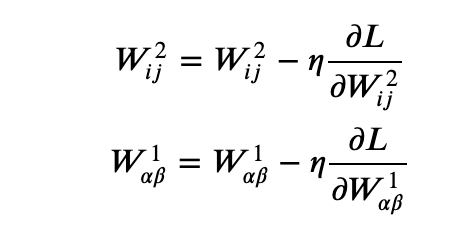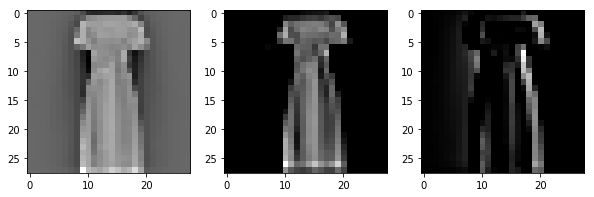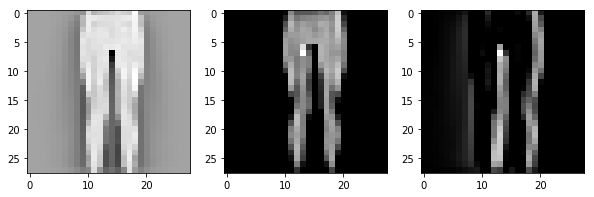In setting out to build Salient we unwittingly assigned ourselves a rather challenging task: designing a system that allows non-technical users to use machine learning to automate simple business processes (related to documents) without requiring them to understand anything about machine learning or even programming. Our hypothesis:
Many (most?) tasks and challenges faced by business users are specific to their organization or their set of documents so they can’t be addressed by simple pre-built and pre-packaged machine learning models.
Rather we wanted to build a system that continuously learns from the users, their documents, and their tasks. Even tasks that are amenable to using pre-trained models will generally benefit from being tweaked by end users: nothing is more infuriating than an automated system that can’t be fixed or corrected!
Of course “users” here could be regular business users or it could be IT engineers training and integrating Salient into their infrastructure. In either case, the goal is for Salient to provide flexible, organization-specific machine learning without requiring any intervention from us (its developers) or even data scientists.
The Challenge(s)
If you start thinking about how to do this you’ll realize the challenges involved are significant:
- Normal users or even IT admins are not data scientists or ML experts so Salient has to be able to manage the plethora of choices and steps required in building a model without user intervention.
- In particular users don’t want to spend a large amount of time labeling documents or generating training data so the process of training the system has to be fast, smooth and feel like a natural part of their workflow. Most importantly users have to quickly see good results otherwise they will not feel motivated to continue using the system.
- We don’t know beforehand (or ever) what the users’ documents will look like so Salient has to be able to support a wide range of document formats, languages and also domain-specific terminology and vocabulary.
- Each client’s task is unique and is not known to us beforehand. The primary use case for Salient is extracting information from or labeling documents but these tasks span a wide range of cases:
- extract specific words or phrases from a sentence based on the meaning of the text
- extract fields from a form based on the visual information (layout of the document)
- label selections of text based on the type of section it is (e.g. clauses in a contract)
In each case we want the system to support a large amount of variability in the input and learn very quickly to generalize to similar documents.
Because of regulatory or security concerns many clients want to run Salient on premise so all the machine learning and other components of the system have to run in a relatively hardware-constrained environment (private corporate clouds are usually expensive) and so be very efficient. In particular, we can’t depend on the presence of GPUs or easily accessible computing power. Our target is to have a single CPU core be able to provide real-time interactive training and inference for a user.
Solving the challenges above has been a very enlightening journey, fraught with painful lessons. In this article I’m not going to dive very deeply into any given problem but rather will focus on the overall architecture we developed to address these problems. Hopefully, I’ll have time later to dig into individual problems and explain some of the interesting things we learned in solving them.
Architecture
This is the architecture for the ML part of Salient (there are several other components involved with document and knowledge management that are not covered here):
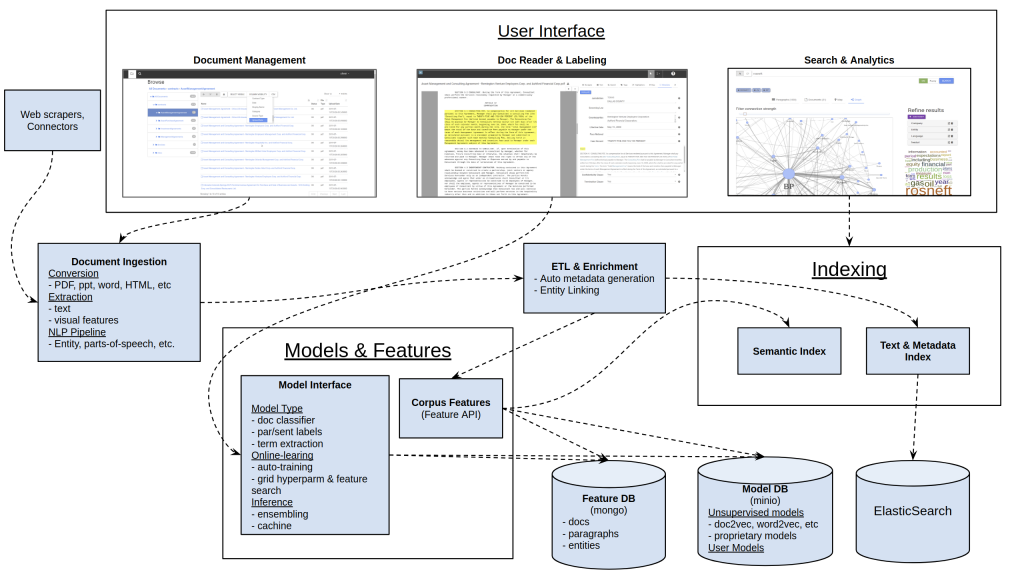
Below I’ll explain the components of the architecture and how they help address the problems above. Hopefully, there’s something in here for you to take away in building your own ML system.
Interface
The elaborate architecture above is invisible to the user or even admin of the system. Instead the user interacts naturally with documents in a nice “smart reader” interface that lets them view, search and extract information from documents:
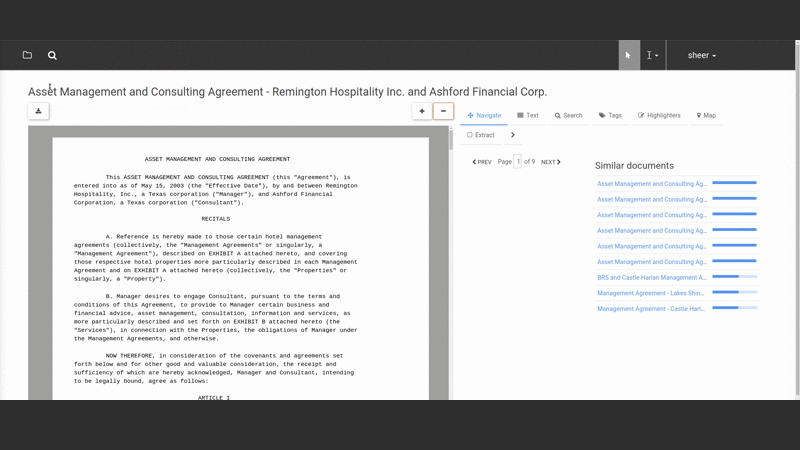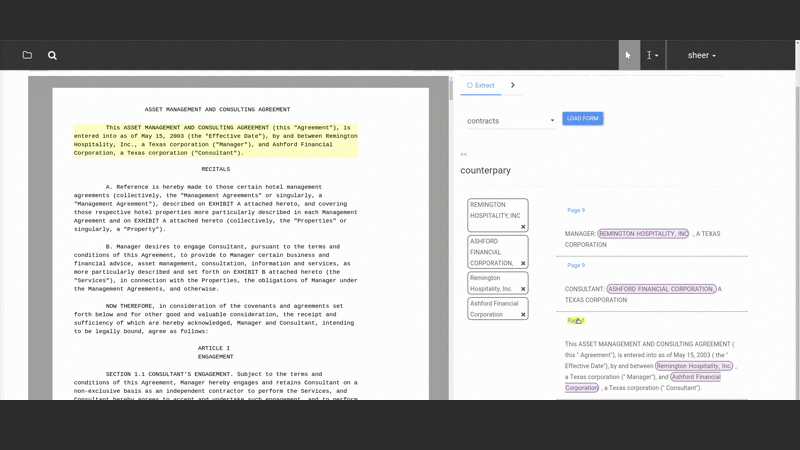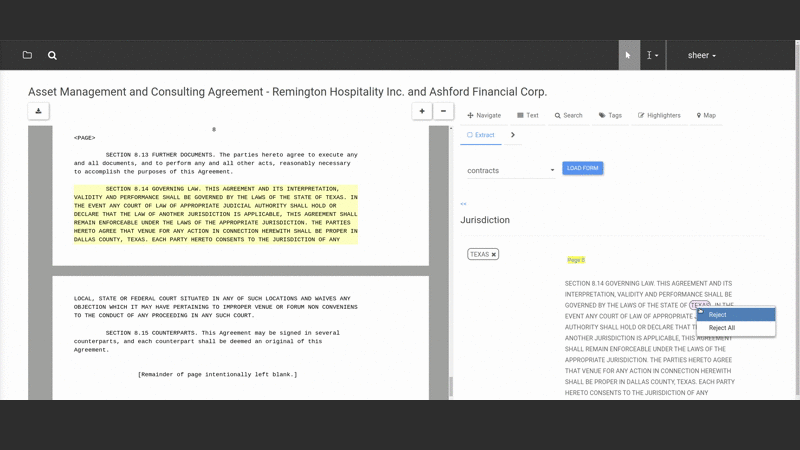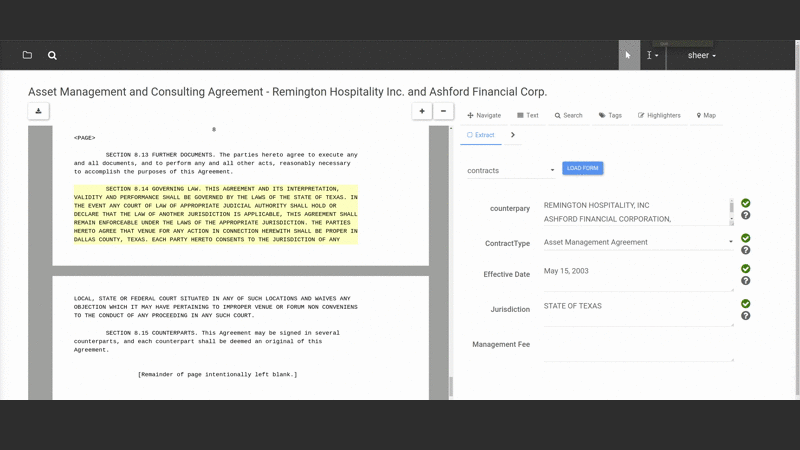
They select text from the document and assign it to fields in a “form” that constitutes the “structured” version of the document (note that both the fields and form are defined by the user — Salient can be taught to extract any kind of data the user wants to extract).
As they do this Salient trains itself automatically in the background, testing and selecting the best models to match the user’s task. When users open a new document Salient can auto-populate the form so the user can evaluate how well the extraction is working and improve it. This interactive process is called “online learning” because the system learns in real-time from user interactions. The ability to quickly see and correct what Salient is learning greatly speeds up the workflow.
Document Ingestion & Processing
This process warrants a whole article on its own but its largely outside the scope of the current discussion. Suffice it to say that document processing can be expensive. Salient reads documents in a range of format, including scanned images that it OCRs, and then converts them to a standardized format that can be rendered in the interactive browser-based view shown above. Salient doesn’t just extract the text from the document but it also tracks layout information as this is an important feature for the ML extraction models. The text of the document is then enriched with the output of a full NLP pipeline (entities, parts-of-speech, etc..). This enriched version of the document is stored in a series of data stores (mongo db, minio, & elasticsearch) so that it can be indexed and used later on.
Model Infrastructure
The machine learning pipeline in Salient runs without user intervention (though users can tweak it if desired). Everything from building unsupervised models and generating features to training and selecting models runs in an automated, distributed pipeline driven by changes of state to the training data (generated by the user) and the document set. This presents some interesting challenges discussed below.
Feature Generation & Caching
Salient makes very heavy use of unsupervised learning. Since our goal is to let users train the system very quickly and efficiently, the more work we can do to help them up-front, the better. To that end, Salient builds a range of unsupervised models (variants of word2vec and our own specialized embedding models) to capture statistical properties of the text, the layout, the entities in the documents, etc.. These features, along with other data about the documents, change quite frequently: the unsupervised models are retrained automatically as more data is added or the data distribution changes and features for new documents are generated as documents are inserted or modified, etc.
All this is computationally expensive so we want to cache the results in a way that can be quickly leveraged when we start to do supervised learning. To that end, we have developed a smart “Corpus Features” data service, built on mongo and minio, that tracks the state of the document corpus, the features for each document and automatically manages rebuilding unsupervised models as needed. We use mongo because it is very flexible (supporting the dynamical needs of such a system) and fast to write and read from and we use minio as blob storage for the models themselves.
Distributing Models
Salient is designed around a distributed stateless worker-based architecture so systems like “Corpus Features” (which can be embedded in any worker) have to be able to intelligently update any worker if e.g. a model changes. To this end all models (supervised and unsupervised) in Salient are tagged with unique ids and a centralized caching system (redis) is used to track the newest version of a model. If one worker updates a model the other workers detect this change and update their local copy of the model to the newest version. This is particularly important for supervised models because a user interacting with the system will generally be hitting several workers (possibly on different servers) so they must have a synchronized state.
Training
Training in Salient can be triggered by a range of events. Models retrain while users are interacting with the system so that users get immediate feedback on what the models have learned. This happens in dedicated background workers so as to not interfere with the user’s workflow but of course any model changes have to be propagated back to the real-time ML inference workers. This is managed by tracking the latest version of each model in a distributed cache and having all workers reload any stale models automatically.
Model retraining can also be triggered by non-user events. For instance, importing a large amounts of new documents can trigger unsupervised models to retrain (to capture the new data distribution) and this will also trigger the supervised models that use them to retrain. This chain of dependencies is managed by generating unique identifiers (UUIDs) on each model training and storing this in any dependent model so we can easily track dependency chains.
Model Selection
For every kind of task (labeling a document, extracting specific text or table entries, etc) Salient has a range of models that are sensitive to different types of features (semantic, structural, visual, local, etc..) and that also have different predictive power. When users have less training data simpler models are favored so they can be retrained faster and be less prone to overfitting.
The selection of features, architecture and training parameters for a model is made by testing many possibilities against user generated data (as part of the background training process) and then selecting the best model based on a “validation set”. This is a (random) subset of the training data that is hidden from the models during training and then used after training to evaluate the performance of each model variant. Not only does this let Salient select the best combination of model, features and parameters but it also provides some indication of how well the model will perform on unseen data. Ultimately Salient selects the best few models for each task and averages their results in an “ensemble”.
All this information about how models have been trained and selected is stored in a training database so that admins can evaluate and understand which models are being used.
Some Technicalities
The discussion and the architecture diagram above cover the conceptual components of the system but not the detailed service or technical architecture. That might be subject a separate post but, in brief, Salient (and the diagram above) is implemented as a distributed job queue with both real-time and batch workers running various stateless mircro-services. This architecture runs in docker-compose or kubernetes but has no other dependencies so it can be deployed in any environment (on the cloud, on-premise). It is, by design, horizontally scalable and fault tolerant.
If you’re interested in learning more about Salient or have some thoughts or questions about the architecture above please don’t hesitate to get in touch!